 zuka
zukaこんにちは。
zuka(@beginaid)です。
本記事はコラムシリーズの1つになります。他のコラム記事は「コラム」カテゴリーページをご覧ください。
 デモデーモ博士
デモデーモ博士今回は,スキーヤーに働く力について説明するぞい!
 パンサーくん
パンサーくん遠心力とかってこと?
 デモデーモ博士
デモデーモ博士そうじゃな。スキー中の力を理解することで,いろいろな動作の必要性が理解できるのじゃ!
 パンサーくん
パンサーくんなんか難しそうだけど,チャレンジしてみる!
物理的な前提
このセクションは,スキーとは直接関係ありませんので,必要でない方は無視して次の「スキーヤーに働く力」に移動してください。
さて,スキーヤーにはたらく力を考える際には,どのような系から事象を観測するかという点が重要になってきます。たとえば,遠心力というのは非慣性系(慣性の法則が成立しない系=加速する物体の上で観測する系)で考えた際の仮想的な力のことを指します。
実際,ターン中にはたらく力を考える際には,スキーヤーと同じ系に乗って考えると分かりやすいので,以下では非慣性系における話をしていきます。
スキーヤーに働く力
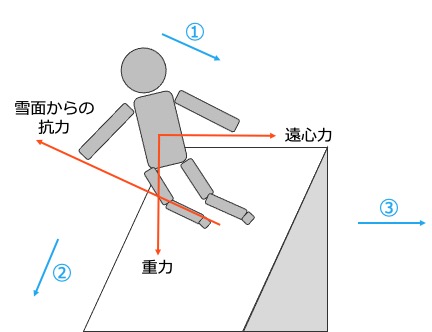
滑走中のスキーヤーには,「重力」「遠心力」「雪面からの抗力」がはたらきます。このうち,重力は常に地球の中心向き,遠心力はターンの外側向きの力になります。
スキーヤーは常に雪面とくっついていますので,①方向の力は全てつりあっています。問題となるのは,②方向と③方向です。それぞれ詳しく見ていきましょう。
②方向
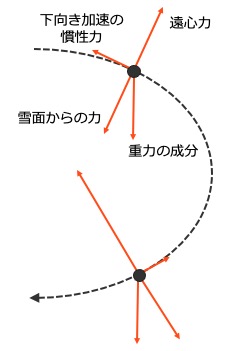
②の視点から見ると,スキーヤーは雪面からの力を向心力とした円運動をしています。また,ターン後半の方が重力の成分が遠心力の味方をしてしまうため,より強い雪面からの力がかかります。
③方向
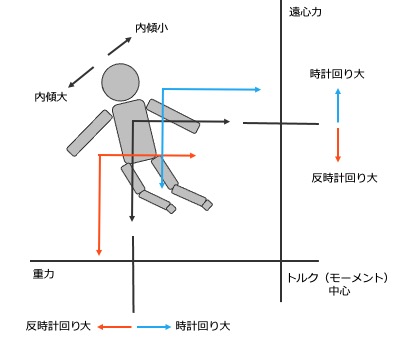
ここからは,スキーヤーを質点ではなく剛体として考えていきます。つまり,スキーヤーはスキー板と雪面の作用点を中心にして,重力と遠心力のトルク(モーメント)がつりあうように重心を移動させる必要があるのです。
仮に,オレンジの状態で遠心力のトルクと重心のトルクがつりあっている状態だとします。一般に,遠心力$F$は「重さ$m$・速さ$v$の2乗」に比例し,「回転半径$r$」に反比例します。
\begin{align}
F &= m \frac{v^2}{r}
\end{align}
ということは,スキーヤーの速さが増していったり,スキー板がたわんで回転半径が小さくなったとき,遠心力は増加します。そのとき,重心は黄色の矢印の位置に移動させる必要があります。なぜなら,黄色の矢印の場所に重心を移動させることで,重心のトルクの腕を長くすると同時に,遠心力のトルクの腕の長さを短くできるからです。
遠心力が減少した場合も同様です。青い矢印の場所に重心を移動させることで,重力のトルクと遠心力のトルクをつりあわせます。
まとめ
 デモデーモ博士
デモデーモ博士お疲れさまじゃ!スキーヤーにはたらく力は理解できたかい?
 パンサーくん
パンサーくんうん!3つの視点で考えると分かりやすいね!
 デモデーモ博士
デモデーモ博士スキーの応用という観点では,③の視点が一番重要じゃな。ターンの理論としては,②の視点で議論されることが多いようじゃ。
 パンサーくん
パンサーくんなんだかスキーって大変なスポーツだね。
[1] 日本スキー教程, 山と渓谷社, 2018.
[2] スキーの科学とスノーボードの科学, 岡部, 2017.


コメント